Andraderivatan
Det är gratis! Vi lär oss beräkna en funktions andraderivata och går igenom hur denna kan användas för att analysera punkter där derivatan är lika med noll. Med hjälp av produktregeln se denna artikel skall det visas att hypotesen är korrekt för samtliga heltal n. Olika områden inom matematiken har dock vanligen en notation som vanligen används. Inom fysiken är derivator vanliga.
Största möjliga värde
I många sammanhang är vi intresserad av att hitta just det största eller minsta värdet som en funktion kan anta. Det finns en enkel minnesregel för att komma ihåg om en andragradsfunktion har en minimipunkt eller en maximipunkt. En sådan funktion saknar därför största och minsta värde i ändpunkterna. I det förra avsnittet undersökte vi växande och avtagande funktioner och hur sådana förändringar hänger ihop med derivatan i olika punkter på en kurva. Även om Leibniz notation kan tyckas något otymplig är den lämplig att använda bland annat vid tillämpning av kedjeregeln och vid lösning av differentialekvationer , på grund av dess tydliggörande av differentialerna. Lokalt maximivärde
En funktion kan anta sitt största eller minsta värde i extrempunkter (maximipunkter eller minimipunkter) eller i intervallets ändpunkter. En funktion kan vara definierad för ett visst intervall och det är i början och slutet av intervallet som är intervallets ändpunkter. När vi bestämmer det största och minsta värdet av en funktion är derivatan till stor hjälp. Lokala maximum eller minimum har inga större respektive mindre värden i närheten.
Derivata exempel
Vi tittar närmare på funktioner och deras grafer, och hur dessa förhåller sig till tangentens lutning. Största och minsta värde I det här avsnittet tittar vi närmare på vad det betyder att derivatan är lika med noll, nämligen extrempunkter. Påminn din lärare om att förnya eller fortsätt plugga med Eddler på egen hand. Slutsatsen vi kan dra av det här är att om vi får andraderivatan till 0 för en extrempunkt, måste vi göra en teckentabell för att avgöra om extrempunkten är ett lokalt maximi-, minimi- eller terrasspunkt. Här går vi igenom andraderivatan. Terrasspunkt
Vi går igenom hur man på ett givet intervall för en funktion kan gå tillväga för att bestämma största och minsta värde (alltså y-värde som funktionen antar). Ange det minsta värdet för funktionen vars graf visas nedan. Om risk för förväxling föreligger kallas derivatan av ursprungsfunktionen förstaderivata. Andragradsfunktion
Study with Quizlet and memorize flashcards containing terms like deriveringsregel polynom, minimipunkt lutning, maximipunkt lutning and more. Kontakta oss på: info eddler. Negativ koefficient framför x 2 x 3 - kurvor Positiv koefficient framför x 3. 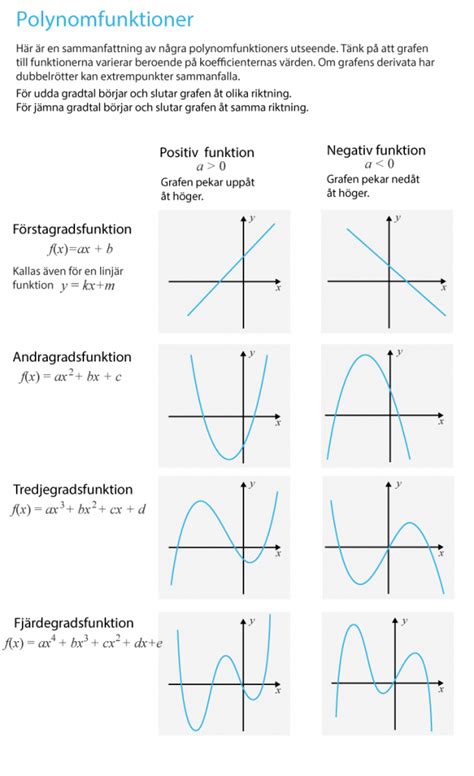
Andragradsekvation exempel
Då man vill bestämma största eller minsta värde samtidigt som man vill uppfylla vissa villkor så kan man använda metoden Linjär optimering. Förutsättningen är att dessa villkoren kan uttryckas som linjära funktionssamband. Därför är det ju rimligt att undra om det inte finns något enklare sätt att komma fram till vilken typ av punkter det rör sig om, annat än att titta direkt på funktionens graf och försöka avgöra frågan därifrån vilket inte alltid är en pålitlig metod. Den andra typen av notation har fått sitt namn efter Gottfried Leibniz. Derivata formel
Deriveringsfel -2p Korrekt beräknat värde på tangentens lutning +1p Deriveringsfel -2p Söker största och minsta värde till funktionen g x ()=− 6 x x -1p Undersöker bara punkter där derivatan är noll -1p Undersöker bara intervallets ändpunkter -2p Svarar med punkter eller med x-värden -1p Utreder ej falska lösningar vid. Punkter på en graf anges som en Koordinat då den motsvarar en position i planet, alltså i två dimesioner. Exempel [ redigera redigera wikitext ].